Maclaurin Series

It's also called Maclaurin polynomials.

Maclaurin series is a special case of Taylor Series which centres at x=0.

image

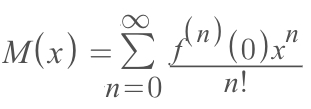
▼Expand it we'll understand it better:

▼Here is a graph we're trying to approximate a function centred at x=0: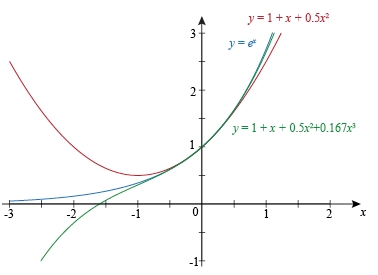

Example

Solve:

• This problem is to test if you're familiar with the Maclaurin Series Formula.

• Let's ignore all others and only see the asked x⁴.

• x⁴ means we're gonna find out the term of the 4th derivative, and plug in 4 into the formula, we'll get the term:

  
• It's asking for the coefficient of x⁴, which is the rest part in that formula for the term:

  
• And we only need to find out what is the value of the 4th derivative.

• By the given formula of gᴺ(0), we can get:

  
• So the coefficient will be:

  

Example

Solve:

• We know the Maclaurin series is a Taylor series centred at x=0, and the formula is: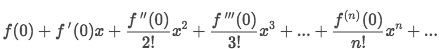

  
• It's told to list 4 terms, so we plug in the given value of f', f'', f''' and get: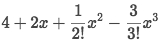

  
• And we get the answer:

  

Evaluate Maclaurin Series

To evaluate a Maclaurin series, we need to convert the series to a function, and then evaluate the function.

▼Jump forward to have a look at the note: Maclaurin Series of Common functions