Improper Integral

After learning Definite Integral, Indefinite Integral, now it's Improper Integral. The major difference between them is their Boundaries.

The improper integral means the integral's boundary or boundaries are infinite, ∞ (or -∞).

Refer to Khan academy: Introduction to improper integrals Refer to Improper Integrals (KristaKingMath)

It looks so fearful yet not too hard to understand.

image

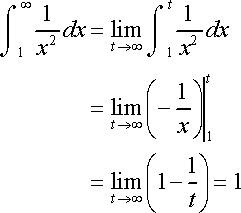
Types of Improper Integral

Refer to video from ProfRobBob: Improper Integrals 5 Examples

There're 6 cases of different improper integral:

• Case 1: From a constant to positive infinity.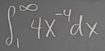

  
• Case 2: From negative infinity to a constant.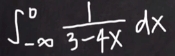

  
• Case 3: From negative infinity to positive infinity.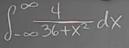

  
• Case 4: From 0 to e.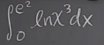

  
• Case 5: From a constant to a constant, but has an infinite discontinuity.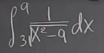

  
• Case 6:

Convergent & Divergent

We can call an improper integral:

• Divergent: When the limit of the improper integral DOES NOT EXIST.

• Convergent: When the limit of the improper integral EXISTS.

Solve Improper Integrals

Basic Strategy:

• Replace the infinite as a variable, etc. t

• Rewrite the expression as taking the limit of the Integral, whereas the t → ∞

• Calculate the Integral with a normal variable first, and gets the result function.

• Calculate the limit of the function

Type 1

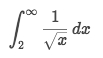Solve:

Type 2

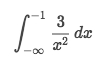Solve:

• Rewrite the improper integral to limit form:

  
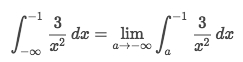
• Do the basic calculation.

• The key point is:

  

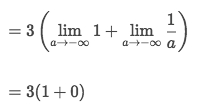
Type 5

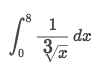Solve: