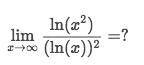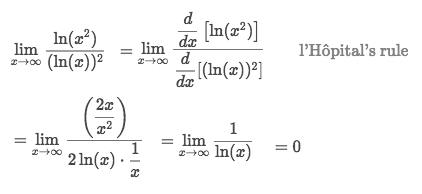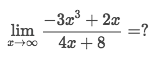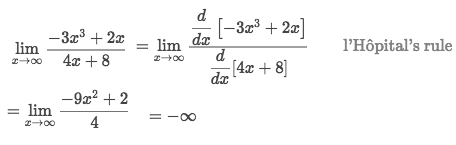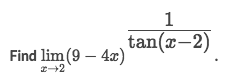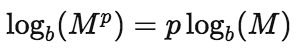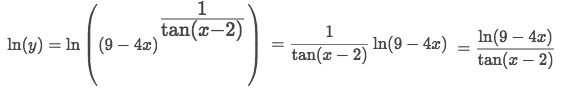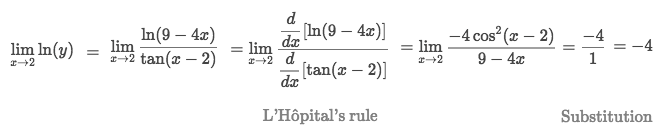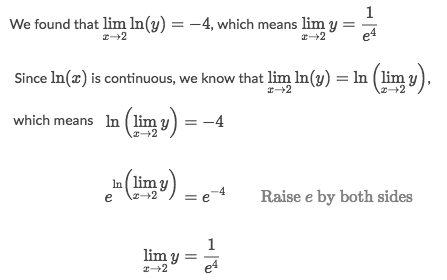L'Hopital's Rule
LHopital's Rule helps us to find the limit of an Undefined limits, like 0/0, ∞/∞ and such. It's quite simple to apply and very convenient to solve some problems.
▶ Back previous note on: Asymptote of Rational Expressions▶ Practice at Khan academy: Disguised derivatives
From my experience, the L'Hopital's Rule is so often been used that we didn't even realize. Actually it's been used almost every time when we are to evaluate the LIMITS OF RATIONAL EXPRESSIONS.
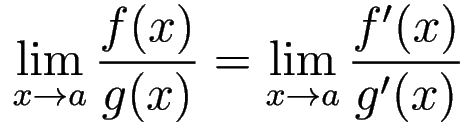
Example of 0/0
0/0Example of ∞/∞
∞/∞Example of 1^∞
1^∞L'Hopital Rule for Composite functions
L'Hopital Rule for Composite functionsExample of composite exponential function
Direct plug in the
x=2and getlimit = 1^∞, which is an indeterminate formSo we're gonna apply the
Log Power Ruleto take down the power:We use Natural Log for doing this:
And now we can apply the
L'Hopital Ruleforln(y):From
ln(y)we could getlimit of y:
Last updated
