Chain Rule
One of the core principles in Calculus is the Chain Rule.
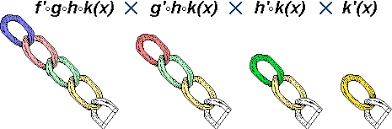
Refer to Khan academy article: Chain rule ▶ Proceed to Integral rule of composite functions: U-substitution
It tells us how to differentiate Composite functions.
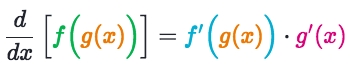
It must be composite functions, and it has to have inner & outer functions, which you could write in form of f(g(x)). 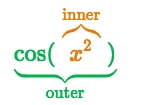
Common mistakes
Not recognizing whether a function is composite or not
Wrong identification of the inner and outer function
Forgetting to multiply by the derivative of the inner function
Computing
f(g(x))wrongly:
How to identify Composite functions
Seems a basic algebra101, but actually a quite tricky one to identify.
Refer to Khan lecture: Identifying composite functions
The core principle to identify it, is trying to re-write the function into a nested one: f(g(x)). If you could do this, it's composite, if not, then it's not one.
Examples
![]() It's a composite function, which the inner is
It's a composite function, which the inner is cos(x) and outer is x².
![]() It's a composite function, which the inner is
It's a composite function, which the inner is 2x³-4x and outer is sin(x).
![]() It's a composite function, which the inner is
It's a composite function, which the inner is cos(x) and outer is √(x).
Two forms of Chain Rule
Two forms of Chain RuleThe general form of Chain Rule is like this: 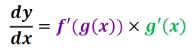
But the Chain Rule has another more commonly used form: 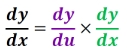
Their results are exactly the same. It's just some people find the first form makes sense, some more people find the second one does.
Example
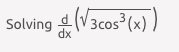 Solve: [Refer to Symbolab worked example.](https://www.symbolab.com/solver/step-by-step/\frac{d}{dx}\left(sqrt\left(3cos^{3}\left(x\right)\right)\right))
Solve: [Refer to Symbolab worked example.](https://www.symbolab.com/solver/step-by-step/\frac{d}{dx}\left(sqrt\left(3cos^{3}\left(x\right)\right)\right))
Chain rule for exponential function
Chain rule for exponential functionFormula: 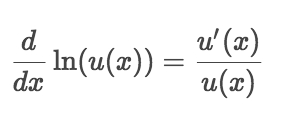
Because: 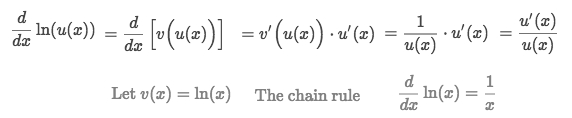
Example
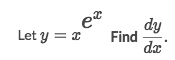 Solve:
Solve:
Apply the
Log power ruleto simplify the exponential function: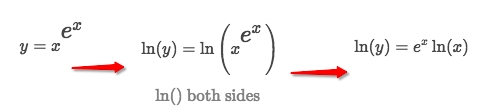
Differentiate both sides:
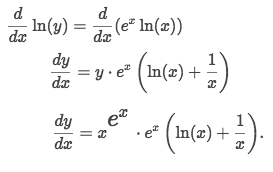
Last updated