Limits at infinity

No matter why kinds of Limits you're looking for, to understand it better, the best way is to read the Step-by-Step Solution from Symbolab: [Limit Calculator from Symbolab.](https://www.symbolab.com/solver/limit-calculator/\lim_{x\to\infty}\left(\frac{6x^{2}-x}{\sqrt{9x^{4}%2B7x^{3}}}\right))

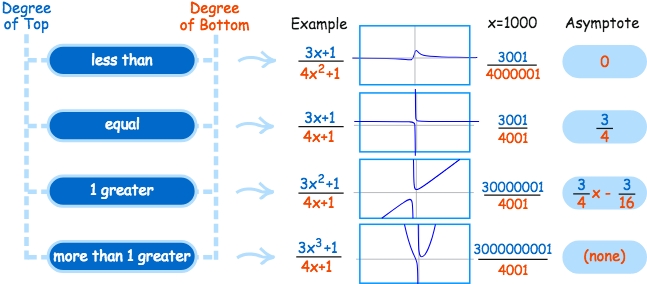
Rational functions

The KEY point is to look at the powers & coefficients of Numerator & Dominator. Just the same with Finding the Asymptote.

Refer to previous note on the How to find Asymptote.

image

Example

Solve:

Quotients with square roots

The KEY point is to calculate both numerator & dominator, then calculate the limit of EACH term with in the square root.

Example

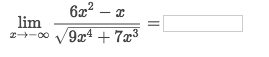Solve: [Refer to Symbolab step-by-step solution.](https://www.symbolab.com/solver/limit-calculator/\lim_{x\to\infty}\left(\frac{6x^{2}-x}{\sqrt{9x^{4}%2B7x^{3}}}\right))

• Divide by highest dominator power to get:

  
• Calculate separately the limit of Numerator & Dominator: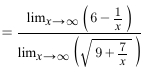

  
• Calculate the Square root: Need to find limits for EACH term inside the square root.

  

  

  
• Then get the result easily.

Quotients with trig

The KEY point is to apply the Squeeze theorem, and it is a MUST.

Example

Solve:

• Know that -1 ≦ cos(x) ≦ 1, so we can tweak it to apply the squeeze theorem to get its limit.

• Make the inequality to: 3/-1 ≦ 3/cos(x)/-1 ≦ 3/1

• Get that right side 3/-1 = -1 and left side 3/1 =1 is not equal.

• So the limit doesn't exist.

Easier solution steps:

• Know the inequality -1 ≦ cos(x) ≦ 1

• Replace cos(x) to ±1 in the equation, 3/±1.

• Calculate limits of two sides.

• If the results are exactly the same, then the limit is the result; Otherwise the limit doesn't exist.

Example

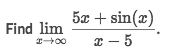Solve:

• Know that -1 ≦ sin(x) ≦ 1

• Replace sin(x) as ±1

• Left side becomes (5x+1)/(x-5), right side becomes (5x-1)/(x-5)

• Both sides' limits are 5, so the limit exists, and is 5.