Alternating Series Test

It's the test for Alternating series.

►Refer to Khan academy: Alternating series test ►Refer to xaktly: Alternating Series

Alternating Series

It means, Terms of the series "alternate" between positive and negative.

etc., The alternating harmonic series:

The Alternating Series Test

image

The very good example of this test is the Alternating Harmonic Series:

image

▲ It does CONVERGES. (But the Harmonic Series does NOT converge)

Strategy:

• Take AWAY the Alternating sign (-1)ⁿ: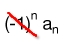

  

• Determine if the rest part is a decreasing series:

  

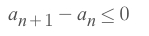
• Take limit of the rest part:

  

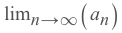
• If Limit = 0, then the series CONVERGES.

• If Limit ≠ 0, then the series DIVERGES.

Example

Solve:

• Notice this is an alternating series, so we're to apply the alternating series test.

• Take away the alternating term, and left with (2/p)ⁿ.

• So the series only converges if (2/p)ⁿ is decreasing and its limit is 0.

• And the only way to make it decreasing is to make sure (2/p) < 1.

• Based on that p value, the limit of (2/p)ⁿ is surely a 0.

• Therefore, p > 2 makes the series converges.

Example

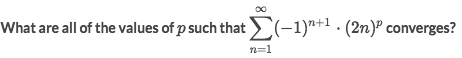Solve:

• Notice this is an alternating series, so we're to apply the alternating series test.

• Take away the alternating term, and left with (2n)ᴾ.

• So the series only converges if (2n)ᴾ is decreasing and its limit is 0.

• And the only way to make it decreasing is to make sure p < 0.

• Based on that p value, the limit of (2n)ᴾ is surely a 0.

• Therefore, p < 0 makes the series converges.