Inflection Point

An inflection point is a point where the graph of the function changes CONCAVITY (from up to down or vice versa).

It could be seen as a Switching point, which means the point that the Slope of function switch from increasing and decreasing. e.g., the function might be still going up, but at such a point it suddenly increases slower and slower. And we call that point an inflection point.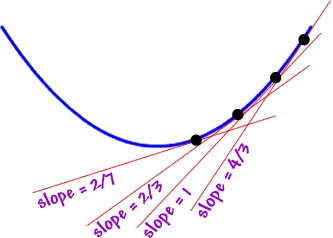

Refer to Khan academy video for more intuition rapidly: Inflection points from graphs of function & derivatives

Algebraically, we identify and express this point by the function's First Derivative OR Second Derivative.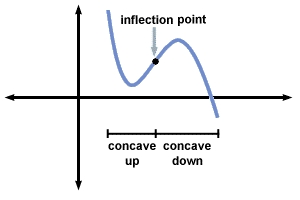

Example

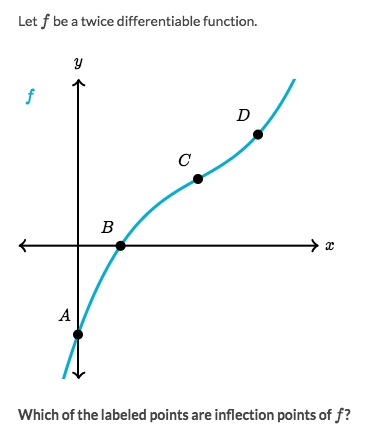Intuitive way to solve:

• Draw a tangent line in imagination and move it on the function from left to right

• Notice the tangent line's slope, does it go faster or slower or suddenly change its pace at a point?

• We found it suddenly changed at point c.

More definitional way to solve:

• Looking for the parts of concavity shapes

• Seems that B-C is a part of Concave Down, and C-D is a part of Concave Up

• So C is a SWITCHING POINT, it's a inflection point.

Example

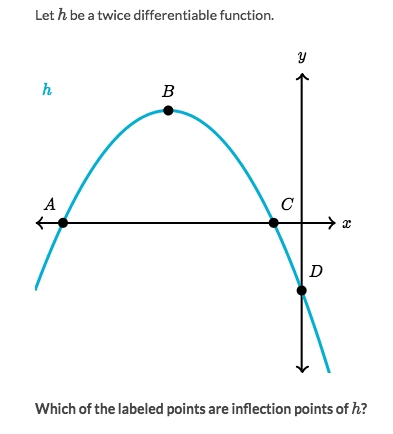Solve:

• Looking for the parts of concavity shapes

• There's no changing of concavity shapes, there's only one shape: Concave down.

Example

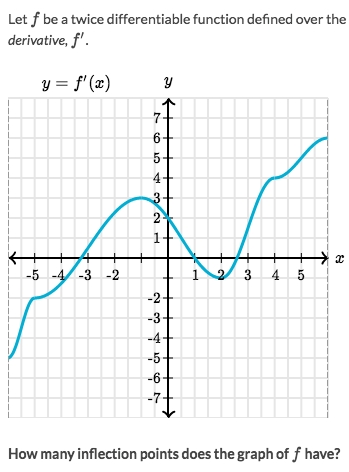Solve:

• Notice that's the graph of f'(x), which is the First Derivative.

• Checking Inflection point from 1st Derivative is easy: just to look at the change of direction.

• Obviously there're only two points changed direction: -1 & 2

Example

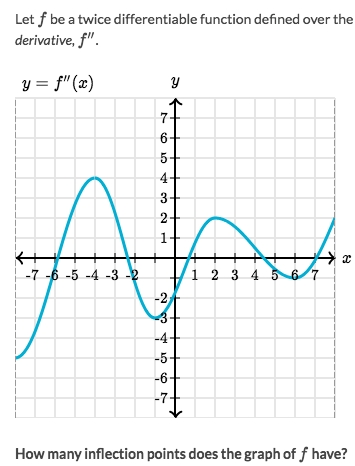Solve:

• Mind that this is the graph of f''(x), which is the Second derivative.

• Checking inflection points from 2nd derivative is even easier: just to look at when it changes its sign, or say crosses the X-axis.

• Obviously, it crosses the X-axis 5 times. So there're 5 inflection points of f(x).

Example: Finding Inflection points

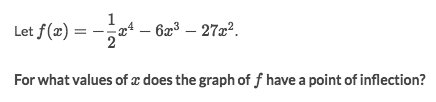Solve:

• Function has POSSIBLE inflection points when f''(x) = 0.

• Set f''(x) =0 and solve for x, got x=-3.

• We now know the possible point, but don't know its CONCAVITY. This need to try some numbers from its both sides:

  
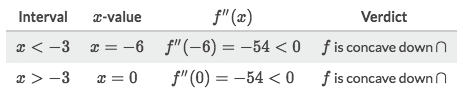
• So it didn't change the concavity at point -3, means there's no inflection point for function.

Example: Finding Inflection points

Solve:

• Function has POSSIBLE inflection points when f''(x) = 0.

• Set f''(x) =0 and solve for x, got x=0 or 6.

  [Refer to Symbolab for f''(x).](https://www.symbolab.com/solver/step-by-step/\frac{d^{2}}{dx^{2}}\left(3x^{5}-30x^{4}\right))

  Refer to Symbolab for f''(x)=0.
• We now know the possible point, but don't know its CONCAVITY. This need to try some numbers from its both sides:

  
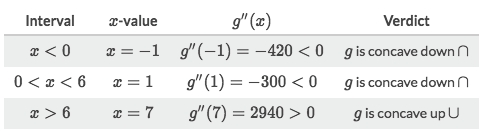
• So it didn't change the concavity at point 0, means only 6 is the inflection point.