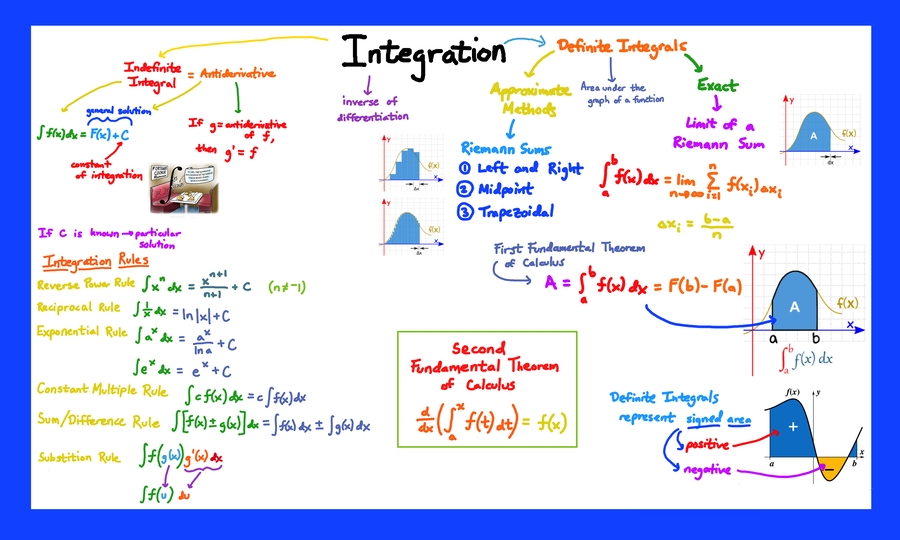
▶️Integral Calculus

Integral calculus is a process to calculate the AREA between a function and the X-axis (or Y-axis).

Core idea of Integral Calculus

Refer to Khan academy: Introduction to integral calculus

image

Riemann Sums

A Riemann sum is an approximation of the area under a curve by dividing it into multiple simple shapes (like rectangles or trapezoids).

Riemann Sums Notation

Refer to Khan academy: Definite integral as the limit of a Riemann sum

image

The letter ʃ (reads as "esh" or just "integral") is called the Integral symbol/sign.

Calculate Riemann Sums

image

Finding 𝚫x: It's meant to get HOW MANY rectangles we're to sum.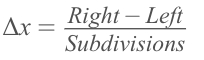

Finding indices m & n: It's meant to find the i for Σ sums:

• For Left Sums or Midpoint Sums: i starts from 0 ends with subdivisions - 1

• For Right Sums: i starts from 1 ends with subdivisions

Finding xi: With equally spaced points (left/right/mid), the xi is a Geometric series of those points, which the rate is the 𝚫x. We're gonna find the right pattern/equation for xi, so that we can plug xi into f(x).

Finding f(xi): Just to plug in the Geometric series expression of xi into f(x), and make it as a function in terms of i.

Left & Right Riemann Sums Approximation

Refer to Maths is fun: Integral Approximations

• Left Riemann Sum: take the Left boundary value of Δx to be the rectangle's height.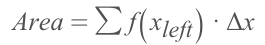

  
• Right Riemann Sum: take the Right boundary value of Δx to be the rectangle's height.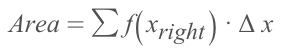

  

image

As you can see, they would be either Over-estimated or Under-estimated. Neither of these approximations would be called a good one, normally.

Midpoint Sums Approximation

It's an enhancement to the Left sums and Right sums, it takes the midpoint value, and sometimes makes better approximation.

image

Example

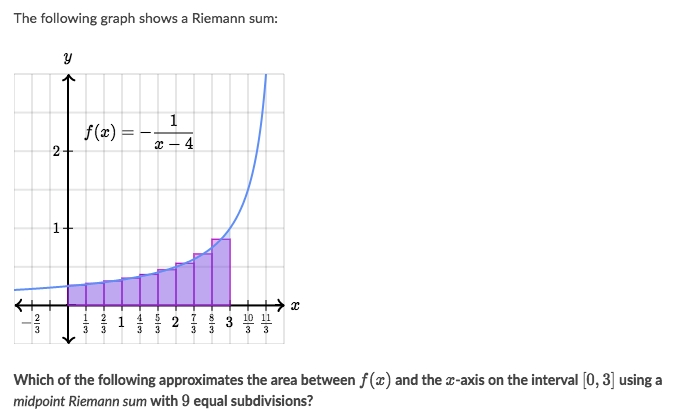Solve:

Example

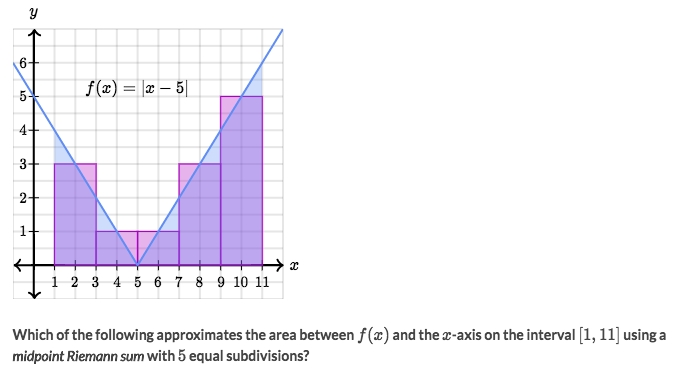Solve:

• It's easy to find the Δx=2.

• Then let's find the f(x𝖎). It's actually a progress to find the Arithmetic Sequence.

• So the sequnce is S(𝖎) = a + 𝖎·Δx = 2 + 2𝖎, where a represents the first x value which is 2.

• So x𝖎 = S(𝖎) = 2+2𝖎

• Takes it back to the function and gets: f(x𝖎) = |2+2i-5| = |2i -3|

Example

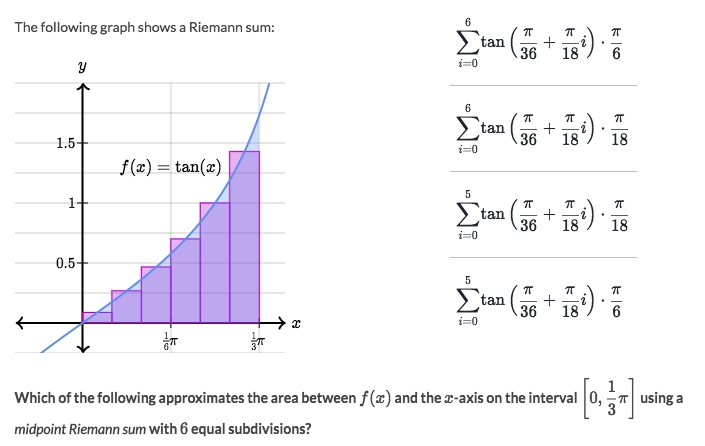Solve:

Example

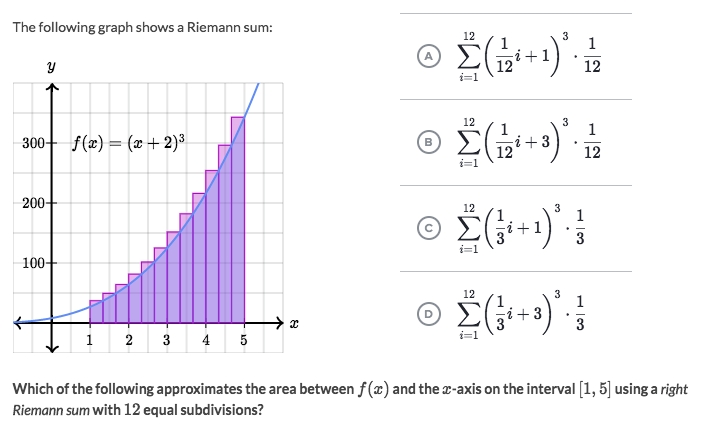Solve:

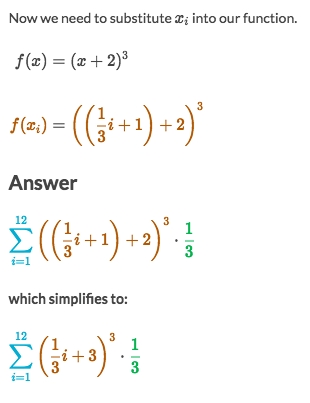
How to calculate Riemann Sums

Refer to Khan academy: Rewriting definite integral as limit of Riemann sum

image

Refer to the Map of Integration: mrozarka.com