Planar motion

It's still the Motion problem but the object not only moves on the X-axis but move in a PLANE, with X-coordinate and Y-coordinate. So it becomes differentiation of vectors. But the differentiation steps are almost the same.

Here are some algebraical expressions:

• Position: P(t) = (x, y)

• Velocity: v(t) = P'(t) = (x', y')

• Acceleration: a(t) = v'(t) = P''(t) = (x'', y'')

Jump to do the Khan academy practice.

Example

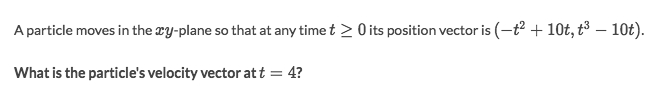Solve:

• Write down all the conditions algebraically:

  • Position: P(t) = (x, y) = (-t²+10t, t³-10t)

  • Velocity: v(t) = P'(t) = (x', y') = (-2t+10, 3t²-10)

  • t=4

• Substitute to get v(4) = (2, 38)

Example

Solve:

• P(t) = (2t²-6t, -t³+10t)

• v(t) = P'(t) = (4t-6, -3t²+10)

• v(2) = (2, -2)

• |v(2)| = √(4+4) = 2√2

Example: Motion along a curve

Refer to Khan academy's quizzes for these practices Solve:

• Position: P(t) = (x, y)

• The rate of change means velocity: v(t) = P'(t) = (x', y')

• Since x' = -2, so it becomes v(t) = (-2, y'). How to get the y'?

• We could find an equation x²y²=16 helps us to get y'.

• It's easier to do implicit differentiation than explicit one:

  (x²y²)'=(16)' -> 2x·x'·y² + x²·2y·y' = 0 -> -4xy² + x²·2y·y' = 0 -> y' = 2y/x

• Substitute (1,4) to the y's rate of change to get y' = 2*4/1 = 8

Example

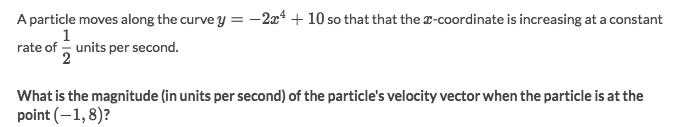Solve:

• P(t) = (x, y)

• x' = 1/2

• v(t) = P'(t) = (x', y') = (1/2, y')

• y'(t) = d/dt (-2x⁴+10) = -2·4·x³·x' = -4x³

• y'(x=-1, y=8) = -4(-1)³ = 4

• So v(t) = (1/2, 4)

• |v(x=-1, y=8)| = √(1/4 + 16)