Specific antiderivatives
Normally the antiderivative is in form of f(x) +C. But actually we could use some additional information to get the C and get the function only in terms of x. And we often call the "additional information" as Initial Conditions, or f₀(x).
Example
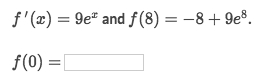 Solve:
Solve:
We could Integrate the
f'(x)to getf(x) = 9eˣ + C.Since
f(8) = 9e⁸ - 8, we could easily see thatC = -8So the function under this condition would be:
f(x) = 9eˣ -8Then we will get the result
f(0) = 9*1 - 8 = 1.
Example
 Solve:
Solve:
We could integrate
f'(x)to getf(x) = x³ - x² + 7x +CSince
f(6)=200, so we could substitute6intof(x):f(6) = 6³ - 6² + 7*6 +C = 200which resultsC = -22So the function under this condition should be
f(x) = x³ - x² + 7x - 22And
f(1) = 1³ - 1² + 7*1 - 22 = -15
Example (Separable equations with specific solutions)
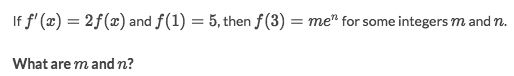 Solve:
Solve:
It looks confusing, but let's assume
f(x)asysody/dx = 2ySeparate differential equations to get
dy/y = 2dxTake integral of both sides:
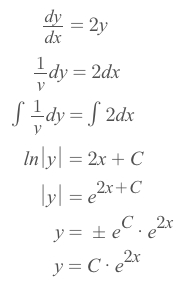
Since
f(1) = 5, so: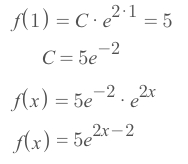
And
f(3) = 5e⁴, which meansm = 5, n = 4
Example
 Solve: Hint:
Solve: Hint: f(0) = 2
Example
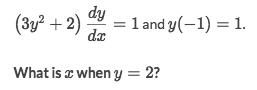 Solve Hint: Don't need to solve
Solve Hint: Don't need to solve y completely. 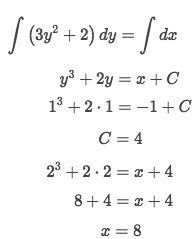
Last updated