Average Value of Functions

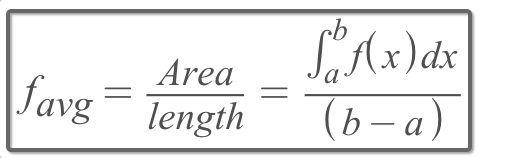
Refer to Khan academy: Average value over a closed interval Refer to video: Average Value of a Function on an Interval

Calculating Favg is just to get the actual area of the function, and then "reform" it to a rectangle, then divide it by its width, then you get the height.

Strategy:

  • Calculate the function's integral, which is the Actual area of the function

  • Calculate the Interval, which is the imaginary rectangle's width.

  • Divide the area by width to get the Average value of function, which is the height.

Mean value theorem for integrals

It actually IS the Average Value of Functions

PreviousTrig-substitutions → Trig RuleNextDifferential Equations

Last updated