Polar Curve Functions (Differential Calc))

▶ Practice at Khan academy.

Refer to Khan academy: Polar functions derivatives

▶ Proceed to: Area of Polar Curves (Integral Calc)

image

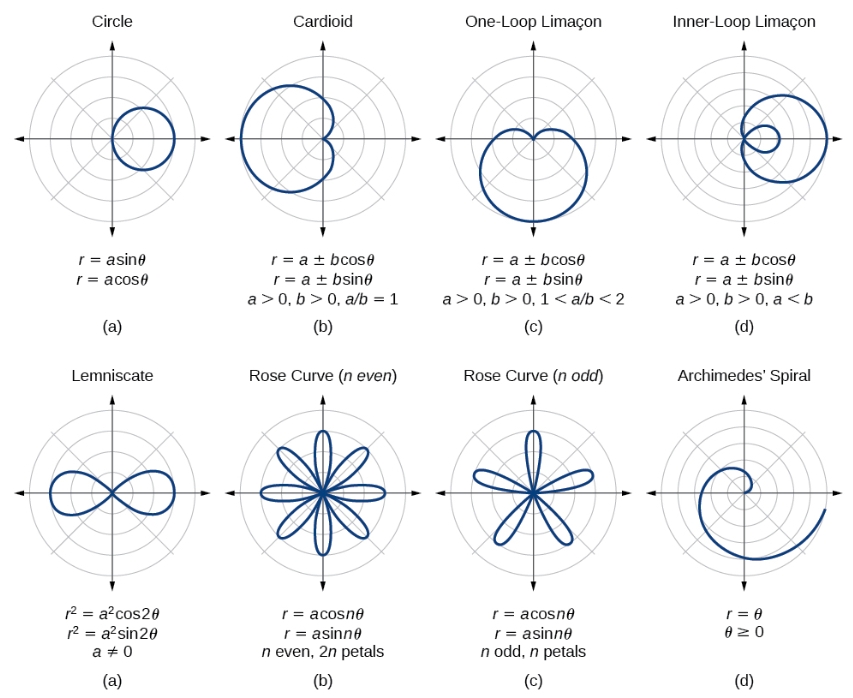
In the Polar World, instead of the relationship between y & x, the function is now representing the relationship between Radius & Angle, which could be presented as:

image

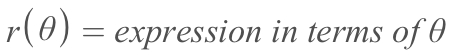
Finding the right boundaries

The most tricky part in Polar system, is finding the right boundaries for θ, and it will be the first step for polar integral as well.

Differentiate Polar Functions

Taking derivative of Polar function is actually DIFFERENTIATING PARAMETRIC FUNCTION. To take the derivative we need to:

• Convert the Polar function in terms of x & y:

  

• Take derivative of the parametric function.

Example

Solve:

• Since it's asking for the Rate of change of y-coordinate, so we convert the polar function to rectangular function:

  

• And we take the derivative dy/dΘ:

  

• Plug in the point Θ=π and get:

  

Tangents to Polar curves

Steps:

• Find the slope dy/dx

• Convert the polar function to get the x(θ) and y(θ) parametric equations

• Solve dy/dx and get the slope

• Plug in the point's information to solve for x & y

• Get the equation of the line (tangent).

Example

Solve:

• To find the tangent line, we need to get the slope first, which is dy/dx.

• And dy/dx would be a parametric problem:

  

• Plug in the Θ value, to evaluate the slope:

  

• Find the x & y value according to the Θ:

  

• Now we got everything to form the equation for the tangent line:

  

  

Example

Solve:

• First, we need to convert the polar function to x(θ) & y(θ):

  

• And we need to find the slope dy/dx:

  

• Since it's a horizontal tangent, so Slope =0, which means dy/dx =0. But dx is dominator can't be zero, so we can set dy = 0 and solve for θ:

  

• So the answer is:

  

Example

Solve:

• To find a vertical tangent, we have to set the dominator of the slope as 0, that's the only thing makes it undefined.

• The slope is dy/dx, so we set dx = 0.

• The equation for x is:

  

  ....