Definite Integrals

DEFINITE means it's defined, means both two boundaries are constant numbers.

Definite integrals properties

Refer to Khan academy article: Definite integrals properties review

image

Definite integral ←→ Limit of Riemann Sum

Example

Solve:

• It's easy to find Δx = (π-0)/n = π/n

• And x𝖎 = S(𝖎) = a + 𝖎·Δx = 0+𝖎·Δx = 𝖎·π/n

• So the result is:

  

Example

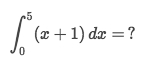Solve:

• Look at the boundaries, it's from 0 -> 5,

• So the Δx must be cut to n pieces, whereas Δx = (5-0)/n = 5/n

• From the definition, We know the function f(x) = x+1

• To fill in the x𝖎 in f(x𝖎), we need to figure out the sequence:

• Sequence x𝖎 = S(𝖎) = a+𝖎·Δx, and since a represents the bottom boundary,

• So x𝖎 = 𝖎(0+Δx) = 𝖎·5/n

• Get x𝖎 back in f(x) to have: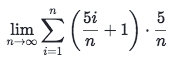

  

Example

Solve:

• We could easily get that the Δx = 5/n

• And the function is f(x) = ln(x)

• Since the Δx comes from Top & Bottom boundaries,

• So Δx = (Top - Bottom)/n = 5/n = (Top - 2)/n,

• And we get the Top = 7, and the Definite Integral is: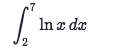

  

Example

Solve:

• See the i=1 means it's using Right Riemann Sum, so the integral would be:

  
• The Δx = 9/n is easily seen.

• And we need to get the Sequence x𝖎 = S(𝖎) = a + (𝖎-1)·Δx = (𝖎-1)·9/n

• What we got there above, tells us a=0.

• According to thatΔx = (b-a)/n = (b-0)/n = 9/n, we get b = 9

• So the answer is: