Optimization

Once you've mastered the Derivatives, you would know the optimization problems are easy. It's just a progress to get the Maximum or Minimum points of a given function.

Example: Max product

Solve:

• It's bit tricky to understand the question.

• Form a function: P(x) = x(a-x) = ax - x²

• To get a maximum, need to find the critical points first.

• Set P'(x) = 0 then get x = a/2.

• To perform a 2nd Derivative Test: P''(x) = -2, means it's Concave Down

• So the critical point a/2 is a maximum.

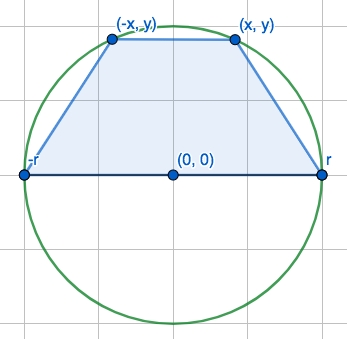
Example: Largest Area of Trapezoid Inscribed in a Semicircle

Q: What is the area of the largest trapezoid that can be inscribed in a semicircle with radius r = 1?

Refer to Kristaking's video: Largest area of a rectangle inscribed in a semicircle

image

Understanding:

• For this Trapezoid inscribed in circle problem, you really want to draw it out before anything else.Refer to this animated tool from Geogebra that I created for this problem.

• Remember that a trapezoid has to have TWO BASES to be parallel.

• Know that, a quadrilateral CAN be inscribed in a circle or even a semicircle, which means 4 vertices are all on the circle.

• A trapezoid of maximum area inscribed in the semicircle will have its base on the X-axis. Which means the length of bottom base should be twice radius: b₁ = 2·r

• Since it's a trapezoid, and inscribed in a circle, then IT HAS TO BE A ISOSCELES TRAPEZOID. And it means it's absolute symmetric about the X-axis.

• With knowing all these conditions above, you could start to abstract the information into equations.

• Get some clue from the result first, then see what's missing and find a way to get it.

Solve:

• First form the equation of trapezoid's area: A = 1/2 · (b₁+b₂) · h

• b₁ is the bottom base, which is equal to 2r = 2, because the largest-area-trapezoid inscribed in circle MUST:

  • lay its base on X-axis

  • equal to the Diameter (because it's the longest base's length)

  • symmetric about the Y-axis (because two bases are parallel)

• Assume one of the vertex on the Top base is (x, y).

• Since the two bases are parallel, so the Top Base is symmetric as well, means it has equal distance to both sides' vertices, which could conclude that:

  • The other vertex on the Top base should be(-x, y).

  • The length of Top Base should be b₂ = x - (-x) = 2x

• The h is hight of the trapezoid, which is equal to the top vertex's y value.

• So the equation then becomes: A = 1/2 · (2r + 2x) · y.

• We need to form a function as Area in term of x, means the Area would change with the change of x. So the y has to transform to the term of x.

• Since (x, y) is a point of the circle, so the circle's Standard formula should work: x² + y² = r²

• Then we get: y = √(r²-x²) = √(1-x²)

• So the final function looks like this: A(x) = 1/2 · (2r + 2x) · √(r²-x²) = (1+x)·√(1-x²)

• Back to the beginning, since we are to find the largest area, so it's saying we are to find the Maximum value of the function A(x).

• Set A'(x) = 0 to find the critical point first. After solve the first derivative by applying product rule, we get: x=-1 or 1/2.

• Since x is a length, so it's a positive value, so x = 1/2. Then y = √(1-x²) = √3/2

• Do the Second derivative test to make sure it's a maximum: A''(x) < 0.

• Substitute the values back to the area equation, we get A = 3√3 / 4

Example: Smallest paper

Solve:

• Assume the area of the inside rectangle (the texts) is T = w · h = 150

• So the area of paper should be A = (w+2)·(h+3)

• Let h = T/w = 150/w

• So the function of area should be A(w) = (w+2)·(150/w +3)

• For getting the area's smallest value, we need to find the critical points first:

• Set A'(w) = 0, and differentiate the function to get: A'(w) = 3 - 300/w², and w=10.

• Substitute the value back to get h=15, So the paper should be (10+2) wide, and (15+3) high.

Example: Largest area of rectangle inscribed in triangle

Solve:

• Form the equation of area of the rectangle: A = w · h

• Apply the Similar triangle property from Geometry lessons, telling that the ratio between two sides are the same with its similar triangle's. So use any of the small triangle there, to form the equation: h/(8-w) = 10/8.

• And we make h = 5(8-w)/4, and the area equation then be A(w) = 5/4 (8w - w²)

• ....