Power Series

Try to think Power series = Geometric Series.

►Refer to Math24: Power series

Power series is actually the Geometric series in a more general and abstract form.

image

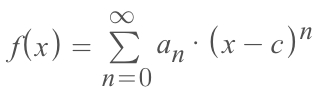
For easier to remember it, that could be simplified as:

image

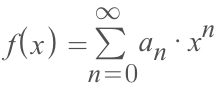
In this function it's critical to know that: a_n IS A CONSTANT NUMBER! NOT A VARIABLE !

Differentiate Power series

►Refer to Khan academy: Differentiating power series

We have 2 ways to differentiate series, they work same way:

• One way is to expand the series with real numbers (1,2,3...) and take their derivatives:

  

  (▲Note that this is constantly true for power series.)

• Another way is to calculate the term's derivative and then plug in the real numbers (1,2,3):

  

Either way will do, it depends on the actual equation for you to choose which way you're gonna use.

Example

Solve:

• Let's organize this function to make it clear:

  

Example

Solve:

• Notice that: If we plug in the x=0 at beginning, everything will be 0 and we don't have anything to calculate.

• So Let's keep the x in the terms until the last step.

• It's easier to expand the series with real numbers, and we're to try 3 or 4 terms in this case.

• Because at the end of it you'll notice, if we're doing Third Derivative, then more than 3 terms will just bring more 0s.

• First we're to organize the function in the standard power series form:

  

• And the constant number a_n in the function is:

  

• Let's plug in the real number (0,1,2,3,4) for n to expand the series:

  

• Based on that we can take the derivatives:

  

• Now we've got the third derivative, so let's plug in the x=0 and see what we get:

  

• And that's the answer.

• And now you know why in this case it's a waste to calculate more terms.

Integrate Power Series

Example

Solve:

• Knowing that Integrate a series can be turned to a series of Integrations of terms:

  

• Integrate the terms:

  

• And we get a simple Geometric series. So that we can apply the formula of calculating geometric series:

  

• Let's apply the formula:

  

Integrals & derivatives of functions with known power series

► Jump over to have practice at Khan academy.

Example

Solve:

• Let's assume the function of the series above is f(x), and the series below is g(x)

• It's clear to see that the g(x) is theAntiderivativeof thef(x)`.

• So we just need to integrate the function of the f(x):

  

• We see that the antiderivative can represent the g(x), but only with the C in it:

  

• So we need to solve for C. The easiest way is to plug in 0 for g(x):

  

• Then the answer is:

  

Example

Solve:

• Set the two series as f(x) and g(x).

• It's clear that g(x) = -f'(x).

• So by differentiate f(x) we will get:

  
• Then -f'(x) would be: