Trig-substitutions → Trig Rule
The goal is to simplify expression by CONVERTING terms of
xinto simplified expression in terms ofθ.
How to do this? We can identify some trigonometric patterns in the expression and apply the Pythagorean Theorem.
▶ Cheatsheet on previous note: Basic Integral Rules ▶ Cheatsheet on previous note: Basic Differential Rules ▶ Cheatsheet on previous note: All trig identities ▶ Back to previous note on: U-substitution → Chain Rule
▶ Practice at Khan academy: Trigonometric substitution
Refer to Khan academy: Introduction to trigonometric substitution
Example
 Solve:
Solve:
In this expression, we can easily identify there is a "pythagorean-like terms":
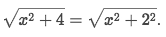
We can see
xand2as two sides of a triangle:
Once we identify the pattern, we can easily get some information out of it in terms of
θ:
From the information
tan(θ)=x/2we can get the relationship betweenx & θ, which is:x=2tan(θ)And now we can convert the original expression to be in terms of
θ:
Example
 Solve: ...
Solve: ...
Last updated