Comparison Test

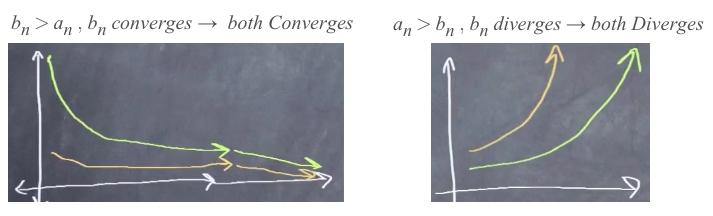
You can understand Comparison Test intuitively as a Sandwich Test.

THIS TEST IS GOOD FOR RATIONAL EXPRESSIONS.

Direct Comparison Test

Assume that we have a series a_n, and we're to make up a similar series to it as b_n:

The logic is:

• If b > a & b converges, then a converges as well.

• If a > b & b diverges, then a diverges as well.

It's so much easier if you think it graphically.

▼Refer to video: Comparison Test (KristaKingMath)

▼Refer to xaktly: Comparison Test

Example

Solve:

• Assume the asked series as a_n, and we make up a very similar series bigger than it, as b_n: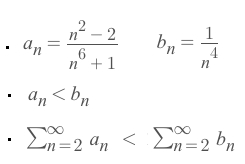

  

• Apply the p-series test we get that the b_n converges.

• Since a_n < b_n, so according to the Sandwich test (Direct comparison test), a_n converges as well.

Limit Comparison Test

Limit comparison test is like an extension when the Direct comparison test won't work. etc., when we compare a with b, although b converges but a > b, so we can't make any conclusion. And that's where the limit comparison test comes in place.

The logic is:

• Take the limit of the division a/b.

• If the Limit > 0, then they both converges or both diverges.

• If the Limit ≤ 0, then there's no conclusion.

►Jump over to Khan academy for practice: Limit comparison test

▼Refer to video: Limit Comparison Test (KristaKingMath)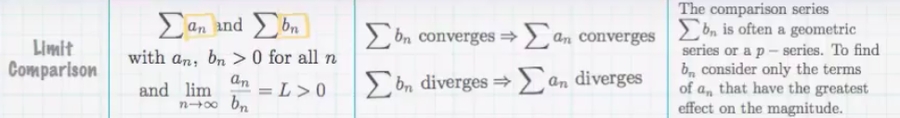

▼Refer to xaktly: Limit Comparison Test

Example

Solve:

Example

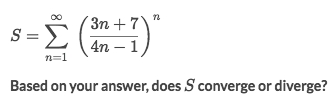Solve:

• We can't easily tell in the comparison who's greater, so we decide to apply the limit comparison test: