▶️Differential Calculus
Simply saying, it's just the SLOPE of ONE POINT of a graph (line or curves or anything).
Refer to Mathsisfun: Introduction to Derivatives
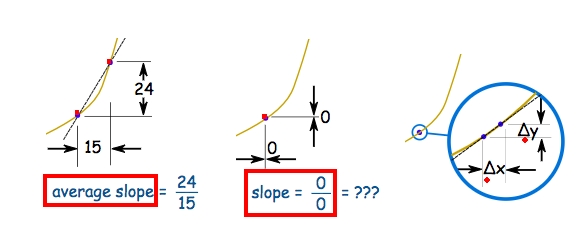
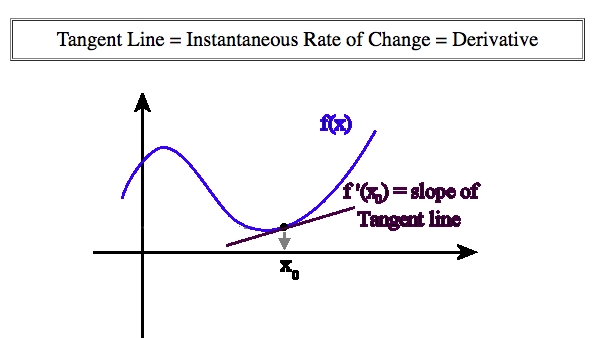
A Derivative, is the Instantaneous Rate of Change, which's related to the tangent line of a point, instead of a secant line to calculate the Average rate of change.
“Derivatives are the result of performing a differentiation process upon a function or an expression. ”
Derivative notations
Derivative notationsRefer to Khan academy article: Derivative notation review.
Lagrange's notation
Lagrange's notationIn Lagrange's notation, the derivative of f(x) expressed as f'(x), reads as f prime of x.
Leibniz's notation
Leibniz's notationIn this form, we write dx instead of Δx heads towards 0. And the derivative of is commonly written as: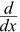 
For memorizing, just see
dasΔ, readsDelta, means change. Sody/dxmeansΔy/Δx. Or it can be represent asdf / dxord/dx · f(x), whatever.
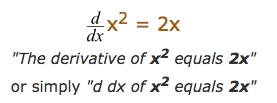
How to understand dy/dx
How to understand dy/dxThis is a review from "the future", which means while studying Calculus, you have to come back constantly to review what the dy/dx means. ---- It's just so confusing. Without fully understanding the dy/dx, you will be lost at topics like Differentiate Implicit functions, Related Rates, Differential Equations and such.
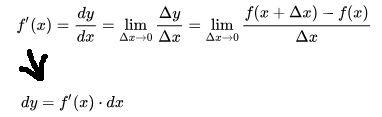
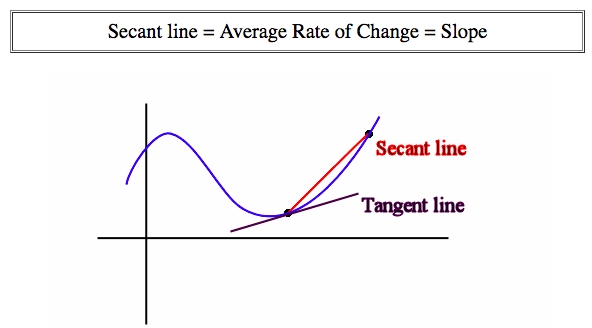
Tangent line & Secant line
Tangent line & Secant lineThe
secant lineis drawn to connect TWO POINTS, and gets us theAverage Rate of Changebetween two points.The
Tangent lineis drawn through ONE POINT, and gets us theRage of change at the exact moment.
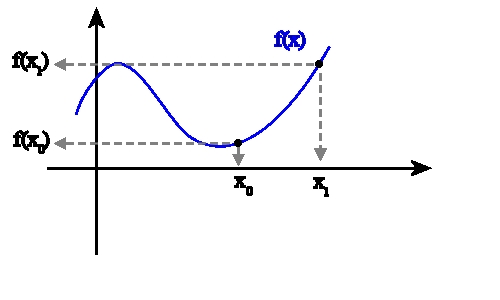
As for the secant line, its interval gets smaller and smaller and APPROACHING to 0 distance, it actually is a process of calculating limits approaching 0, which will get us the tangent line, that been said, is the whole business we're talking about: the Derivative, the Instantaneous Rate of Change.
Secant line
Example
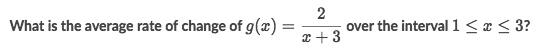Solve:
What it's asking is the
Slope of its secant line:
which could be applied with this simple formula:
the result is
( f(3)-f(1) )/ (3-1) = -1/12
Last updated