U-substitution → Chain Rule

The u-substitution is to solve an integral of composite function, which is actually to UNDO the Chain Rule.

▶ Back to previous note on: Chain Rule

Compare how we handle the composite functions with derivatives & integrals:

• For taking the derivative of a COMPOSITE function, we apply the Chain rule.

• For taking the integral of a COMPOSITE function, we apply the u-substitution.

Refer to Khan academy: 𝘶-substitution: defining 𝘶

We use u-substitution when we need to integrate an expression of the form of: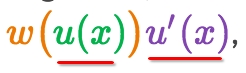

Strategy:

• Find a function as u

• Find or MAKE an u' at the outside so that you can pair u' with dx

• Replace u' · dx with du, because u' = du/dx

• Rewrite the Integral in term of u, and calculate the integral

• Back substitute the function of u back to the result.

image

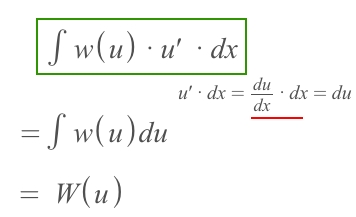
How to select u

Selecting u is the most tricky part here.

Example

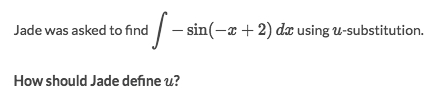Solve:

• Apparently, we ignore the wrapper sin() here.

• We notice that the derivative of -x+2 is -1 which we could find it at outside.

• So let u = -x+2 and u' = -1

• So rewrite the integral to ʃ sin(u) · u' · dx = ʃ sin(u) · du

• It looks quite neat, so the u = -x+2 is alright.

Example

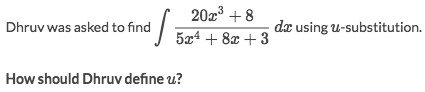Solve:

• Apparently it's in form of ʃ u'/u · dx

• So that we can make u'·dx = du and the integral becomes ʃ 1/u · du

• Quite nice, so the answer would be out of there.

How to calculate Indefinite Integral with u-substitution

Example

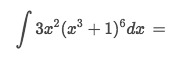Solve:

• With a real quick eyeballing, we see it's in form of ʃ u' · u⁶ · dx

• So with u' · dx = du we will get the simplified form ʃ u⁶ · du = u⁷/7

• Back substitute function of u back to get the result:

  

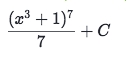
How to calculate Definite Integral with u-substitution

Example

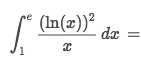Solve: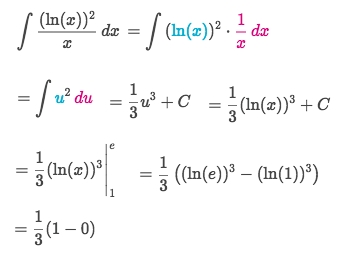

Example (self-made u')

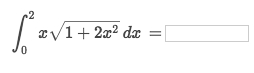Solve: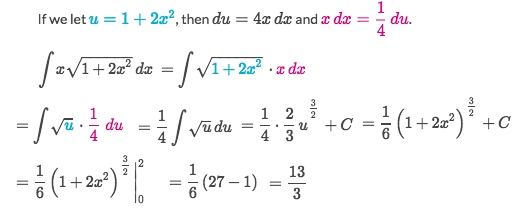

Example (Inverse Trig Rule)

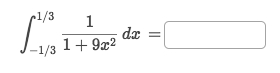Solve:

• Notice this radical form should directly use the Reversed Inverse Trig Rule:

  
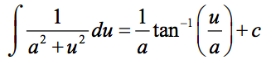
• So that we assume a = 1 & u = 3x.

• Since u' = 3 so we need to make a 3 from nowhere.

• Rewrite the formula to: 1/3 ʃ 3/(1+u²) ·dx = 1/3 ʃ 1/(1+u²) ·du

• Apply the Reversed Inverse Trig Rule to get: 1/3 arctan(u) + C

• Back substitute 3x to u and the boundaries back to x get the result π/6.