Fundamental Theorem of Calculus (FTC)
This is somehow dreaded and mind-blowing. But it's the only thing to relate the
Differential Calculus&Integral Calculus.
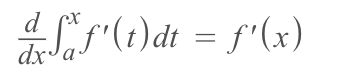
It's so much clearer if you see the function in the middle of integration as a derivative.
Notice that: In this theorem, the lower boundary a is completely "ignored", and the unknown t directly changed to x.
►Refer to Khan academy: Fundamental theorem of calculus review ►Jump over to have practice at Khan academy: Contextual and analytical applications of integration (calculator active).
1st FTC & 2nd FTC
1st FTC & 2nd FTCThe Fundamental Theorem of Calculus could actually be used in two forms. They have different use for different situations.
(Notice that boundaries & terms are different)
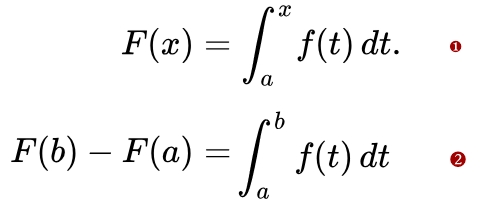
How to Differentiate Integrals
How to Differentiate IntegralsWe could CONVERT the integral formula to Differential formula, by using the fundamental theorem of calculus, and use the Rules we've learnt to solve the differential equations.
Refer to video from Krista King: PART 2 OF THE FUNDAMENTAL THEOREM OF CALCULUS!
We got different strategies for different boundaries situation:
A variable and a number.
A function and a number.
Two functions.
▼ Here is formulas for different boundaries of integration:
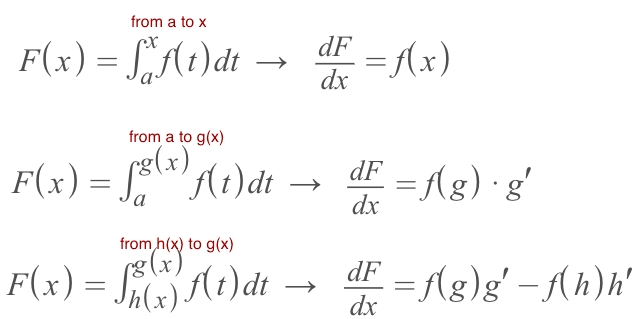
Example
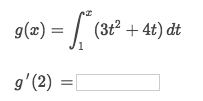 Solve:
Solve:
It's to apply the
boundary situation strategyofA variable & a number:G'(x) = g(x)Assume the function in the middle of integral is
G'(x) = 3x²+4xSince it's asking for
g'(x), so it's differentiate the Integral:d/dx ʃ G'(x) dtexpressionSo
g'(2) = G'(x) = 3x²+4x = 20
Example
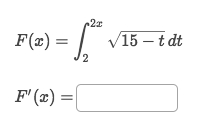 Solve:
Solve:
According to the different
Boundary situation strategies, here we apply theA function & a numberstrategy:F'(x) = f[g(x)] · g'(x)So
F'(x) = √(15 - 2x) · (2x)' = 2√(15-2x)
Example
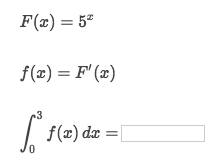 Solve:
Solve:
It's asking you to apply the FTC in form of
d/dx ʃ f'(x) dx = f(b) - f(a)So it becomes calculating
F(3) - F(0) = 125 - 1 = 124
Example
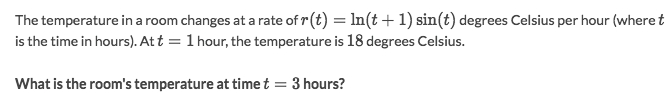 Solve:
Solve:
We could use the
Second Fundamental Theorem of Calculus: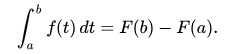
which in this case is:
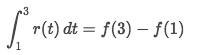
And we move the known terms to one side and keep the asking term at another side:
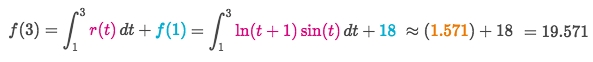
Last updated