Separable Differential Equations

This section is an essential method for solving differential equations. Especially about the initial condition, it is the critical information for getting the original function.

Example

Solve:

• No we can't. Because:

  

Example

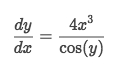Solve:

• First to transfer same terms to the same side.

• Then take integral of each side

• Operate to get y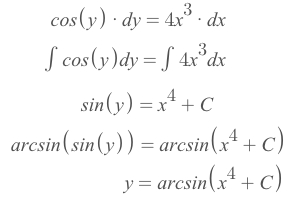

  

Example

Solve:

• We could easily get the derivative of second equation is y' = -2/3.

• Let's see if two of the derivatives are equal by substitute back the y expression: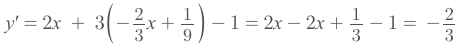

  

• Clearly they're equal. So the answer is YES.

Example

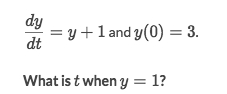Solve:

• Move the same terms to each side:

  
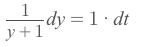
• Take integral of both side:

  
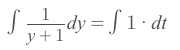
• Get that:

  
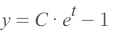
• Plug in y(0) = 3 to get C=4, so the equation then be: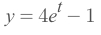

  
• Set y=1 and get t = ln(1/2) = -ln(2)

Exponential model equations

►Jump to Khan academy for practice

►Refer to Khan academy: Worked example: exponential solution to differential equation

Example

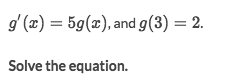Solve:

• Rewrite the equation, and take integral of both side:

  
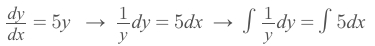
• And we get:

  
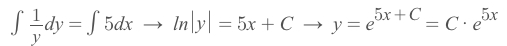
• Let's plug in g(3)=2 to solve for C: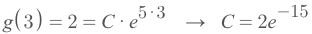

  
• Take C back and get the equation for g(x):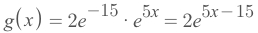

  

Example

Solve:

• We are told that the rate of change of P is proportional to P, which means in Math is:

  
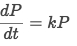
• It's clear that is a Differential Equation, and we rewrite them and take integral of both side to get: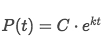

  
• Solve for C: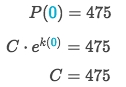

  
• Solve for k: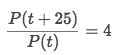

  
• get the k: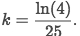

  
• Now we have the full equation, and get the result: