Interval of Convergence
When we see the series as a function, we can actually specify an interval for the function so that the series certainly converges over this interval.
►Jump over to have practice at Khan academy: Interval of convergence
The method is kind of like finding the interval of an ordinary function:
The
termof series can't be0, so seta_n ≠ 0and solve it to get the condition.Take some
convergence tests, etc.ratio test.Calculate to get the condition that makes the test passes.
Substitute the
endpointsof the interval back in the function and see if it also converges.
Example
 Solve:
Solve:
The term can't be zero, so:
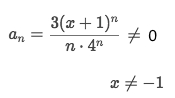
And further more, take a
ratio testwhich makes it converges: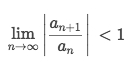
Calculate the
ratio testto get the interval: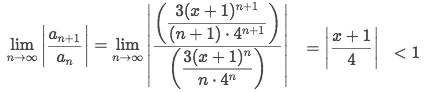
Get the interval for
x: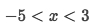
Test the
endpointsfor this interval: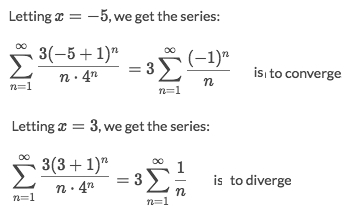
In conclusion, the
interval of convergenceis: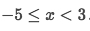
Last updated