Existence Theorems

Existence theorems includes 3 theorems: Intermediate Value Theorem, Extreme Value Theorem, Mean Value Theorem.

Refer to Khan academy: Existence theorems intro

image

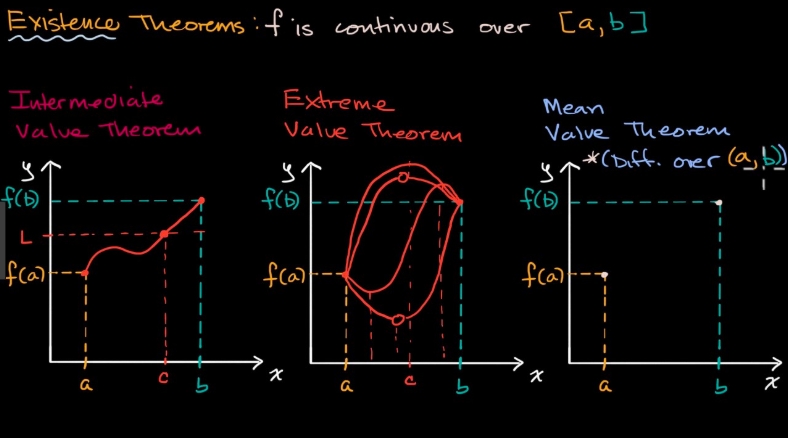
Intermediate Value Theorem (IVT)

The IVT is saying:

When we have 2 points connected by a continuous curve: one point below the line, the other point above the line, then there will be at least one place where the curve crosses the line!

image

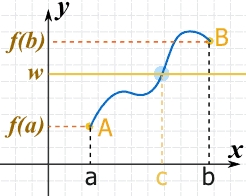
Refer to Maths if fun: Intermediate Value Theorem Refer to video: Intermediate Value Theorem Explained

Find roots by using IVT

IVT is often to find roots of a function, which means to find the x value when f(x)=0. So for finding a root, the definition will be:

If f(x) is continuous and has an interval [a, b], which leads the function that f(a)<0 & f(b)>0 , then it MUST has a point f(c)=0 between interval [a,b], which makes a root c.

Example

Tell whether the function f(x) = x² - x - 12 in interval [3,5] has a root. Solve:

• We got that at both sides of intervals: f(3)=-6 < 0, and f(5)=8 > 0

• So according to the Intermediate Value Theorem, there IS a root between [3,5].

• Calculate f(c)=0 get the root c=4.

Extreme Value Theorem (EVT)

The EVT is saying:

There MUST BE a Max & Min value, if the function is continuous over the closed interval.

image

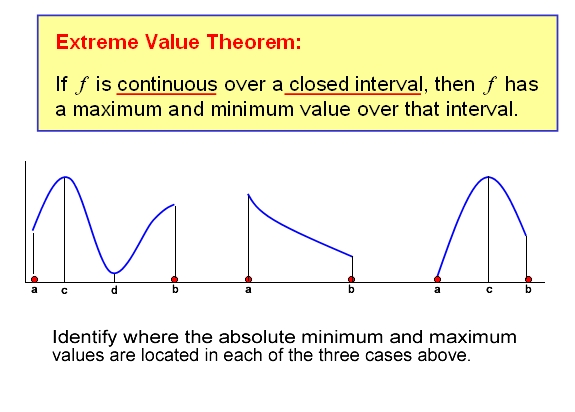
Refer to Khan lecture: Extreme value theorem Refer to video: Extreme Value Theorem

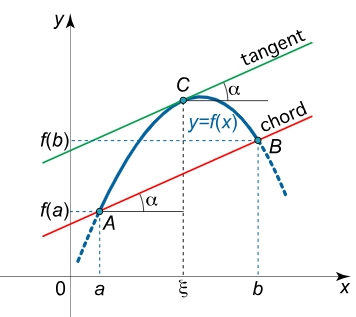
Mean Value Theorem (MVT)

Refer to Khan academy article: Establishing differentiability for MVT

The MVT is saying:

There MUST BE a tangent line that has the same slope with the Secant line, if the function is CONTINUOUS over [a,b] and DIFFERENTIABLE over (a,b).

Which also means that, if the conditions are satisfied, then there MUST BE a number c makes the derivative is equal to the Average Rate of Change between the two end points.

Equation

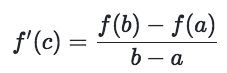
Conditions for applying MVT:

• Continuous over interval (a, b)

• Differentiable over interval [a, b]

Graph

Example

Solve:

• He's totally right.