Slope Field
▶ Refer to Khan academy: Worked example: range of solution curve from slope field
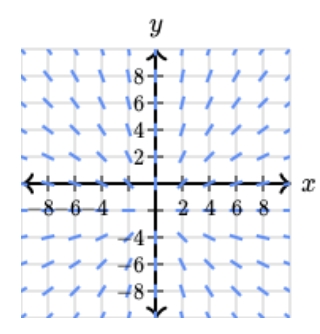
Example
 Solve:
Solve: 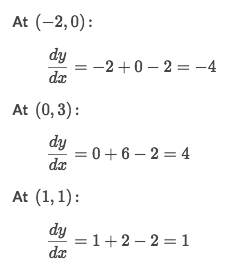
Example
 Solve: Hint: Try a point or points in each quadrant, like Q1: (2,2), Q2: (-2,2), Q3: (-2,-2), Q4: (2,-2)
Solve: Hint: Try a point or points in each quadrant, like Q1: (2,2), Q2: (-2,2), Q3: (-2,-2), Q4: (2,-2)
Let's only try the point
(2, 2), we will gety' = 0, which means the line in Q1 would be horizontal.
Example
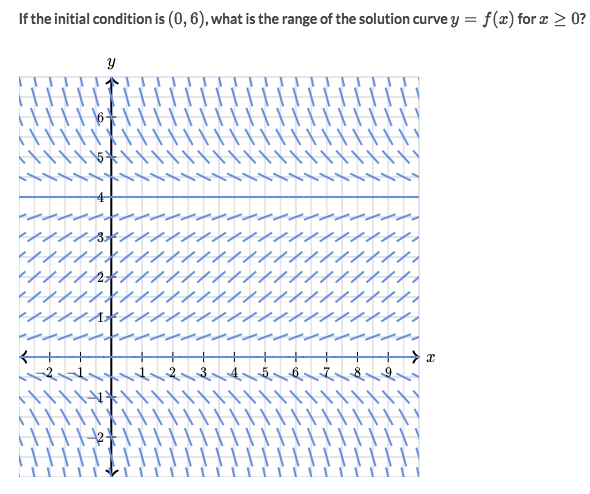 Solve:
Solve:
Since
6is the initial condition, so we make6as a boundary.The slope at
(0,6)is a negative slope, which seems keeps negative until4.So the Range would be
(4, 6].
Example
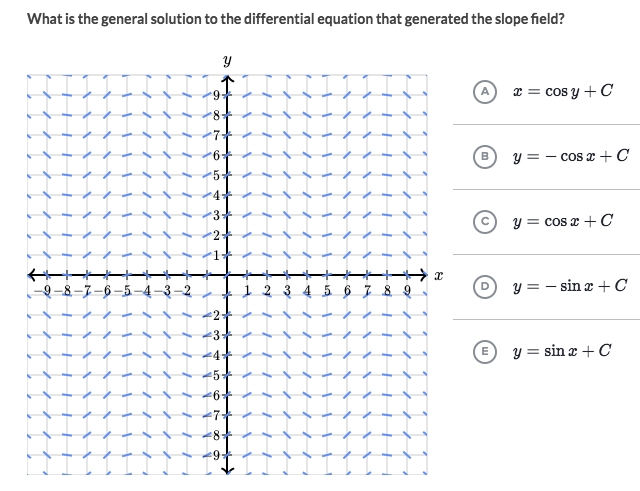 Solve:
Solve:
Try out a point, etc, the initial point is
(0, 1).TAKE DERIVATIVE of each equation, to get the SLOPE of each.
Plug in the
x=0value to get each slope, and eyeball it.
Last updated