Antiderivatives

That's easier being said, THE ANTIDERIVATIVES IS THE INDEFINITE INTEGRALS.

Let's make it more intuitive (might not be accurate but good for learning):

• Antiderivatives is the RESULT.

• Indefinite integrals is the OPERATION.

(They're saying the same thing)

And, just for refreshing:

• Anti-derivatives: Means the Original function where the derivative is from.

• Indefinite integrals: Indefinite means not-defined, means both BOUNDARIES are not defined. That's why the symbol is without any number but ʃ alone.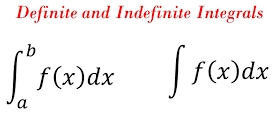

  

Why is the Indefinite Integral so confusing

It's a simple reason: Because they use the f(x) in the Integral expression, but actually it means f'(x)!

You all know the expression of indefinite integral is ʃ f(x) dx, But actually it should be ʃ f'(x) dx, which means the function appears in the middle is a derivative, from somewhere. And the mission of that integral, is to find the f(x) the original function of the derivative!

So trust me, the world would be much nicer if you always see it as the expression as below:

image

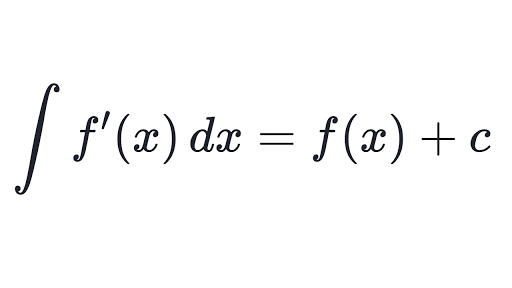
Why is Antiderivative so confusing too

Because your first impression of the antiderivative is that is it anti- something? Anti- is a reverse, derivative is also a transform of something, so putting them together is really a horrible idea because it seems leading to nowhere.

Now here is the mojo, things would be much nicer if you see and call an antiderivative as: The original function f(x)

It may not be accurate, but good enough to proceed to next stage of study.

Review of Antiderivatives

Before you proceed to the next, you really want figure out completely what an antiderivative means with respect to the Integration.

!! Refer to video from The Organic Chemistry Tutor: Antiderivatives

Here are a few examples to quick review what is antiderivative:

image

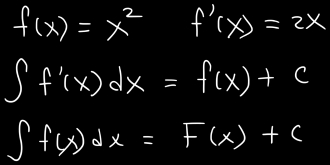
How to understand this reverse process

Doing an Integration, is actually to find the antiderivative.

At the example below, you will find it makes so much sense if you FIX YOUR EYES only onto the MIDDLE part of the integration formula, the part between ʃ & d/dx.

image

Example

Solve:

• First need to clear your mind, in this case:

  • The antiderivative is the "original function" f(x) we have learned.

  • The function f(x) here is actually the derivative, which is f'(x) we've learned.

• Just think it as matching function and its derivative, everything will be tackled real quick.

Example

Solve:

• First need to make sense of the terms:

  • The function appears in the Integral expression, is actually the derivative

  • The "result" is just the Original function where the derivative comes from, or you could call the result is the antiderivative.

• Just think it as matching function and its derivative, everything will be tackled real quick.