Differentiability

"If the point of a function IS differentiable, then it MUST BE continuous at the point."

Example of NOT differentiable points: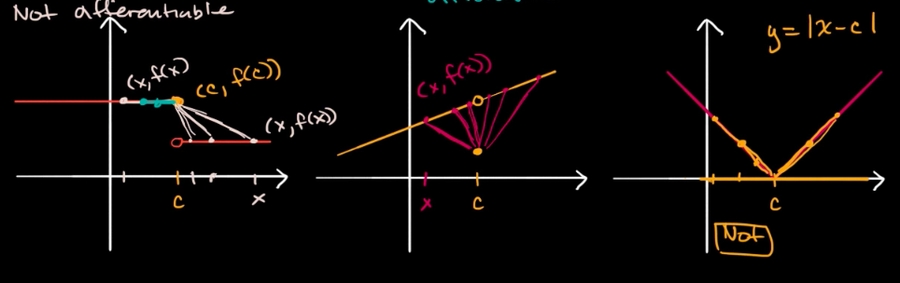

You can see, if the point DOES NOT have limit, it's NOT DIFFERENTIABLE. In another word, the point is not CONTINUOUS, it's Jump Discontinuity, or Removable Discontinuity, or any type of discontinuities.

Not differentiable situations

• Vertical Tangent (∞)

• Not Continuous

• Two sides' limits are different

image

Vertical Tangent

We know that the Slope of Vertical Tangent is UNDEFINED, on the contrary: IT IS A VERTICAL TANGENT, IF:

• The derivative dy/dx = undefined, or

• The denominator of derivative's expression = 0.

Horizontal Tangent

It's a Horizontal Tangent, if:

• dy/dx = 0.