Integral Test

►Jump over to have practice at Khan academy: Integral test. Refer to article from tkiryl: The Integral Test Refer to Khan academy: Integral Test

▼Refer to awesome article from xaktly: Integral Test

image

image

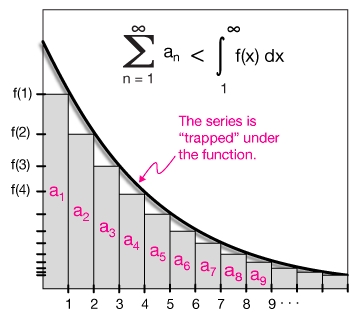
Conditions of Integral test

Assume the series a𝖓 can be represented as a function f(x). There are a few limitations for it to use the Integral test:

• f(x) MUST BE continuous.

• f(x) > 0. It MUST BE a positive function.

• f'(x) < 0. It's MUST BE decreasing.

Using Integral test

image

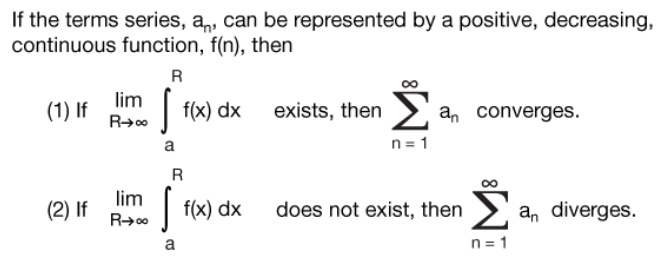
Example

Solve:

Understanding Integral test

The Integral test has introduced the idea of calculating the total area under the function:

• The series has step of 1, which means Δx = 1

• We can sum the areas (which equals the series itself):

  
• But when we are to INTEGRATE the function area under the function:

  
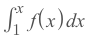
• The dx is infinitely small rather than a fixed number Δx = 1.

• As result, the INTEGRAL is almost always greater than the SERIES AREAS.

As been said above, we got this conclusion: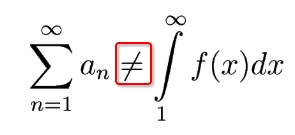

Notice: DO NOT use the Integral Test to EVALUATE series, because in general they are NOT equal.