Partial fractions → Log Rule
A technique for integrating
Rational functions.
▶ Jump back to previous note on Partial fractions.
▶Refer to Khan academy: Partial fraction expansion to evaluate integral
Example
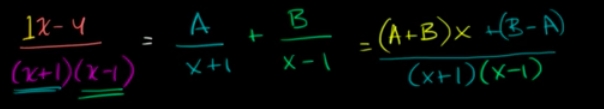 This process is to break down the
This process is to break down the Rational Function to some simple fractions, which assume there are A & B leads to a system of equation:
(A+B)·x + (B-A) = 1·x + (-4)So
(A+B) = 1and(B-A) = -4, which gets usA = 5/2&B = -3/2
Strategy:
Look at the
Nominator&Dominator's degrees.If the dominator's degrees are higher or equal than the nominator, we do
Long division of polynomialto downgrade it.Try to
factorizethedominatorif you can.Assume two variables
A & BApply the
Partial Fraction Expansiontechnique.
Apply the basic
Log Ruleto solve the parts.
Example
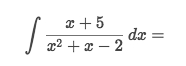 Solve:
Solve: 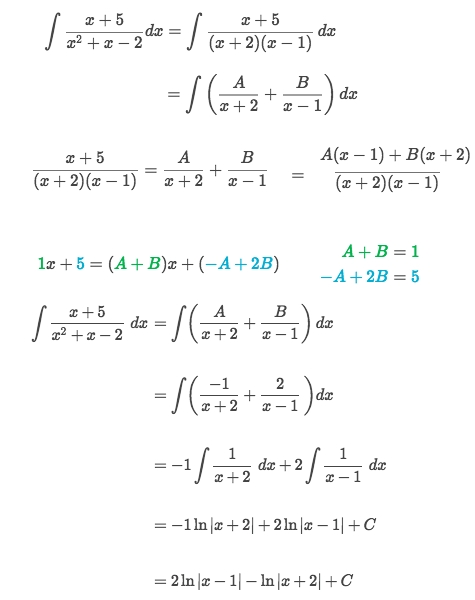
Example
 Solve: Refer to Symbolab.
Solve: Refer to Symbolab. 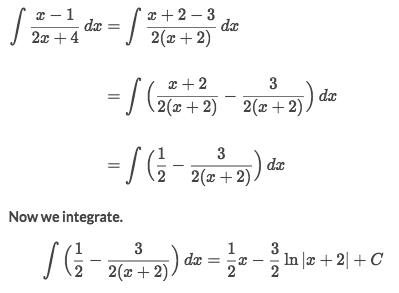
Last updated