▶️Series (Calculus)
►Jump back to previous note: Series (High school level)
Explicit Sequence vs. Recursive Sequence:
Explicit sequence would be presented as:
a𝓃 = a₁ · kⁿ⁻¹. Recursive sequence would be presented as:a₁ = 3, a𝓃 = k · a𝓃₋₁
Sequence vs. Series:
Sequence is a LIST of numbers, Series is a NUMBER: the SUM of a sequence.
Convergence vs. Divergence:
Convergence means the limit of a function EXISTS. Divergence means the limit DOES NOT EXISTS.
Geometric Series in 𝚺 Notation
Geometric Series in 𝚺 Notation▼Refer to Cool Math: Geometric Series 
Example
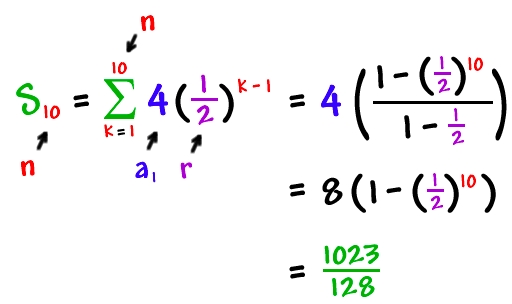
Infinite Sequence (convergence | divergence)
Infinite Sequence (convergence | divergence)►Jump to practice: Sequence convergence/divergence
Example
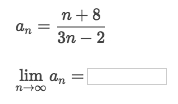
Easiest way: Apply the `L'hopital's Rule, take both Top's & Bottom's derivatives until both of them become numbers.
So we get:
1/3.
Finite Geometric Series
Finite Geometric Series►Jump to practice: Finite geometric series
Example
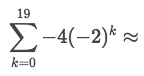 Solve:
Solve:
By using the
Geometric Series formula, we get the informations as below:Common ratio:
r = -2Amount of items:
n = 20. Becausekstarts from 0, so there're 20 terms.Initial term:
a₀ = -4
We calculate and get the result as below:
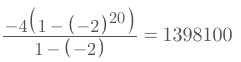
Partial Sums
Partial SumsPartial sums is just a fancy word for Finite series, because it's a a part of infinite series.
Example
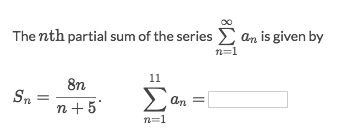 Solve:
Solve:
The tricky part is how to count the amount of terms.
Since
nstarts from 1, so there're 11 terms, which means we're to calculateS₁₁.S₁₁ = 88/16 = 11/2
Example
 Solve:
Solve:
The tricky here is that:
a𝓃 = S𝓃 - S𝓃-1, becauseS𝓃 = a₁ + a₂ + a₃ +.... + a𝓃-1 + a𝓃.So the result is:
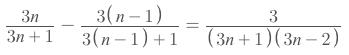
Last updated